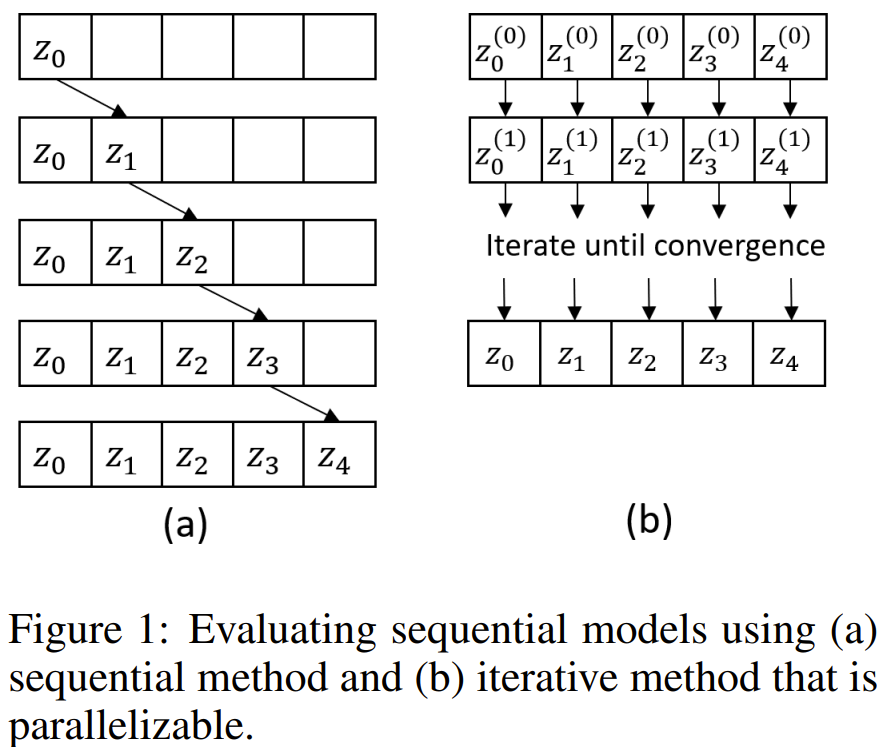
基于牛顿求根法，新算法实现并行训练和评估RNN，带来超10倍增速

人们普遍认为 RNN 是无法并行化的，因为其本质上的序列特性:其状态依赖于前一状态。这使得人们难以用长序列来训练 RNN。近日，一种新算法的出现打破了这一惯常认知，可以并行化 RNN 和 NeuralODE 等非线性序列模型的评估和训练，从而为相关研究和开发带来显著的速度提升。

过去十年来，深度学习领域发展迅速，其一大主要推动力便是并行化。通过 GPU 和 TPU 等专用硬件加速器，深度学习中广泛使用的矩阵乘法可以得到快速评估，从而可以快速执行试错型的深度学习研究。

尽管并行化已经在深度学习研究中得到了广泛的使用，但循环神经网络（RNN）和神经常微分方程(NeuralODE)等序列模型却尚未能完全受益于此，因为它们本身需要对序列长度执行序列式的评估。

序列评估已经变成了训练序列式深度学习模型的瓶颈。这一瓶颈可能会使人们关注的研究方向偏离序列模型。

举个例子，注意力机制和 transformer 在近些年中超过 RNN 成为了语言建模的主导技术，部分原因就是它们能以并行的方式训练。连续归一化流（CNF）过去常使用的模型是 NeuralODE，现在却转向了训练过程不涉及到模拟 ODE 的新方向。

近期有一些尝试复兴序列 RNN 的研究工作，但它们的重心都是线性循环层 —— 可使用前缀扫描（prefix scan）来进行并行化地评估，非线性循环层在其序列长度上依然无法并行化。

近日，英国 Machine Discovery 公司和牛津大学的一篇论文提出了一种新算法，可将 RNN 和 NeuralODE 等非线性序列模型的评估和训练工作并行化，并且他们宣称这一算法还不会在「合理的数值精度」内改变模型的输出。

论文地址:https://arxiv.org/pdf/2309.12252.pdf

那么他们是怎么做到这一点的呢?

据介绍，他们引入了一种用于求解非线性微分方程的通用框架，其做法是将这些方程重新表述为二次收敛的定点迭代问题，这相当于牛顿求根法。定点迭代涉及到可并行运算和一个可并行地评估的逆线性算子，即使是对于 RNN 和 ODE 这样的序列模型也可以。

由于是二次收敛，所以定点迭代的数量可以相当小，尤其是当初始起点接近收敛的解时。在训练序列模型方面，这是一个相当吸引人的功能。由于模型参数通常是渐进式更新的，所以之前训练步骤的结果可以被用作初始起点。

最重要的是，研究者表示，新提出的算法无需序列模型具备某种特定结构，这样一来，用户不必改变模型的架构也能收获并行化的好处。

DEER 框架:将非线性微分方程视为定点迭代

DEER 框架具有二次收敛性，并且与牛顿法存在关联。这一框架可以应用于一维微分方程（即 ODE），也可用于更高维的微分方程(即偏微分方程 / PDE)。该框架还可以应用于离散差分方程以达到相同的收敛速度，这一特性可以应用于 RNN。

使用该框架，用户可以设计一种用于评估 RNN 和 ODE 的并行算法，并且不会对结果产生明显的影响。

DEER 框架

令我们感兴趣的输出信号为 y （r），其由 n 个在 d 维空间的信号构成，其坐标表示为 r。输出信号 y (r) 可能依赖于输入信号 x (r)，其关系是某个非线性的延迟微分方程(DE):

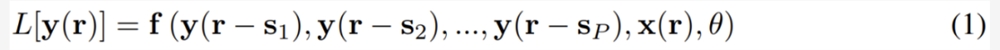
其中 L [・] 是 DE 的线性算子，f 是非线性函数，其依赖于 P 个不同位置的 y 值、外部输入 x 和参数 θ 的。这是一个通用形式，足以表示各种连续微分方程，比如 ODE（当 L [・] = d/dt 且 r = t）、偏微分方程(PDE)、甚至用于 RNN 的离散差分方程。

现在，在左侧和右侧添加一项

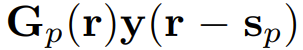
，其中 Gp （r） 是一个依赖于位置 r 的 n×n 矩阵。G_p 的值会在后面决定。现在1式就变成了:

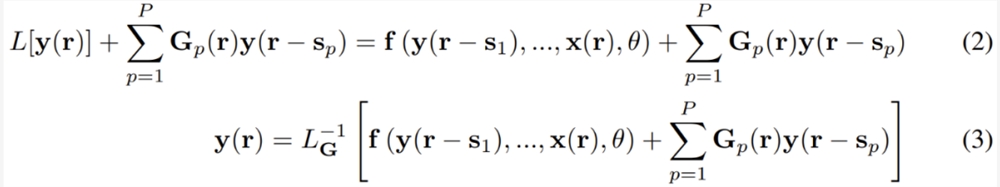
2式的左侧是一个关于 y 的线性方程，在大多数情况下，其求解难度都低于求解非线性方程。在3式中，研究者引入了一个新符号

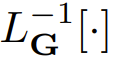
，用以表示在给定边界条件下求解2式左侧的线性算子的线性算子。

3式可被看作是一个定点迭代问题，即给定一个初始猜测

，可以迭代地计算等式右侧，直到其收敛。为了分析这种接近真实解的收敛性，这里将第 i 轮迭代时的 y 值记为

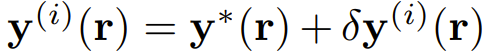
，其中

是满足3式的真实解。将 y^（i） 代入3式可以得到 y^(i 1)，然后泰勒展开至一阶，得:

其中 J_pf 是 f 在其第 p 个参数上的雅可比矩阵。根据上式，通过选择

可让 δy^（i 1） 的一阶项为0。

这表明，根据上式选择矩阵 G_p，能以最快的速度收敛到解附近。这还表明，3式和5式中的迭代相当于在巴拿赫空间（Banach space）中实现牛顿法，因此能提供二次收敛性。

3式中的迭代过程涉及到评估函数 f、其雅可比矩阵和矩阵乘法，这些运算可以使用现代加速器（如 GPU 和 TPU）来并行化处理。如果能以并行方式求解线性方程，那么整个迭代过程都可利用并行计算。在深度学习背景中，将非线性微分方程视为定点迭代问题来求解还有另一个优势，即可以将前一步骤的解(如果能放入内存)用作下一训练步骤的起始猜测。如果起始猜测更好，则能减少寻找非线性微分方程的解所需的迭代步骤。

实际实现

为了将3式的 DEER 框架用于具体问题，需要遵循一些步骤。

第一步是将问题改写成1式，定义变量 y、线性算子 L [・] 和非线性函数 f （・）。

第二步是实现研究者所说的位移器函数（shifter function）。这个位移器函数是以 y (r) 的整体离散值为输入，返回经过位移的 y 值的列表，即 y (r − s_p)，其中 p = {1， ...， P}。这个位移器函数可能需要一些附加信息，比如起始或边界条件。这个位移器函数的输出将会是非线性函数的输入。

下一步（通常也是最难的一步）是根据矩阵列表 G_p 和在某些点离散的向量值 h 实现逆算子

。这个逆算子可能也需要有关边界条件的信息。

只要能提供算法1中的需求，就可以将 DEER 框架应用于任意微分或差分方程。

并行化常微分方程（ODE）

ODE 的形式通常是 dy/dt = f （y (t）， x (t)， θ)，其中初始条件 y (0) 是已给定的。上面的 ODE 形式如果用1式表示，则有 r = t、L = d/dt、P =1和 s_1=0。这意味着 ODE 中的算子

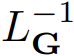
相当于在给定初始条件 y （0） 时求解下面的线性方程。

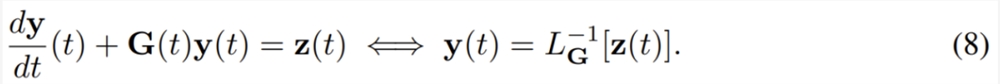
假设 G （t） 和 z (t) 是 t = t_i 和 t = t_{i 1} 之间的常量，分别为 G_i 和 z_i，则可以将 y_{i 1}=y_(t_i 1) 和 y_i = y (t_i) 之间的关系写成:

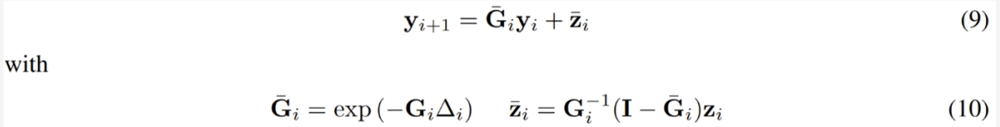
其中 ∆_i = t_{i 1} − t_i，I 是单位矩阵，exp （・） 是矩阵指数。9式可以使用并行前缀扫猫算法进行评估。具体来说，首先可以为每个离散时间点 t_i 定义一对变量

，初始值 c_0=（I|y_0） 以及一个关联算子

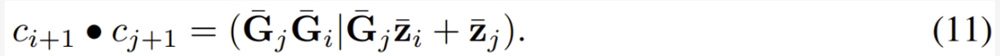
给定上面的初始值 c_0和关联算子，可以并行方式运行关联扫描以获取上述算子的累积值。解 y_i 可从这个并行扫描算子的结果的第二个元素获取。

并行化 RNN

循环神经网络（RNN）可以看作是一种离散版的 ODE。令索引 x 处的输入信号为 x_i，前一状态为 y_{i-1}，则当前状态可以写成 y_i = f (y_{i-1}， x_i ， θ)。

这个形式可以捕获常见的 RNN 单元，比如 LSTM 和 GRU。而如果用1式来写这个形式，则有 r = i、L [y] = y、P =1和 s_1=1。这意味着给定起始状态 y_0，可以通过求解下式来计算逆线性算子:

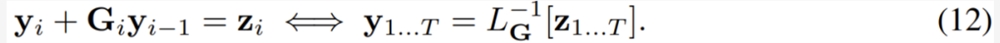
求解上式就相当于求解前一小节的9式。这意味着也可以使用并行前缀扫描和11式中定义的关联算子来将其并行化。

实验

图2给出了新提出的方法在 V100GPU 上所实现的速度提升。

这张图表明，当维度小、序列长度长时，取得的速度提升最大。但是，随着维度增多，速度提升会下降。对前向 梯度计算的提速甚至超过仅前向计算的提速。

图3比较了使用序列方法和 DEER 方法评估的 GRU 的输出。

从图3可以看出，使用 DEER 方法评估的 GRU 的输出几乎与使用序列方法获得的输出一样。图3（b） 中的小误差源于单精度浮点的数值精度限制。

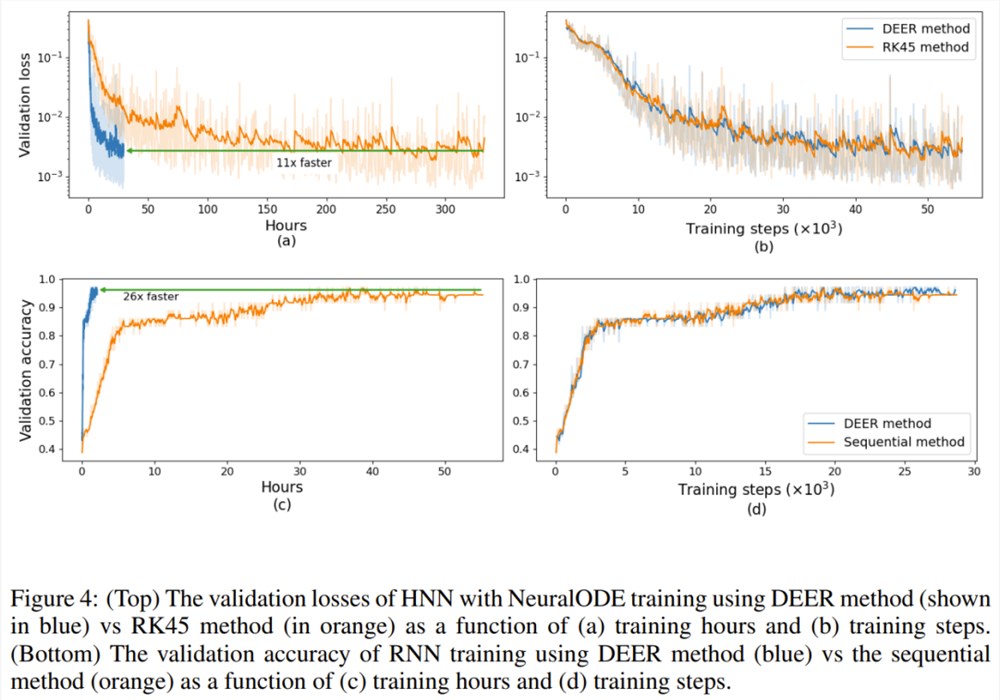
图4（a， b）. 给出了使用 DEER 方法和 RK45方法时训练期间的损失变化情况。从图中可以看到，相比于使用普通的 ODE 求解器，当使用新提出的 DEER 方法时，训练速度可以提升11倍，并且这两种方法的验证损失差别不大。

图4（c， d） 比较了使用 DEER 方法和常用的序列方法时，GRU 网络训练期间的验证准确度。从图中可以看到，使用 DEER 方法时的验证准确度图表与使用序列方法时的很相近。